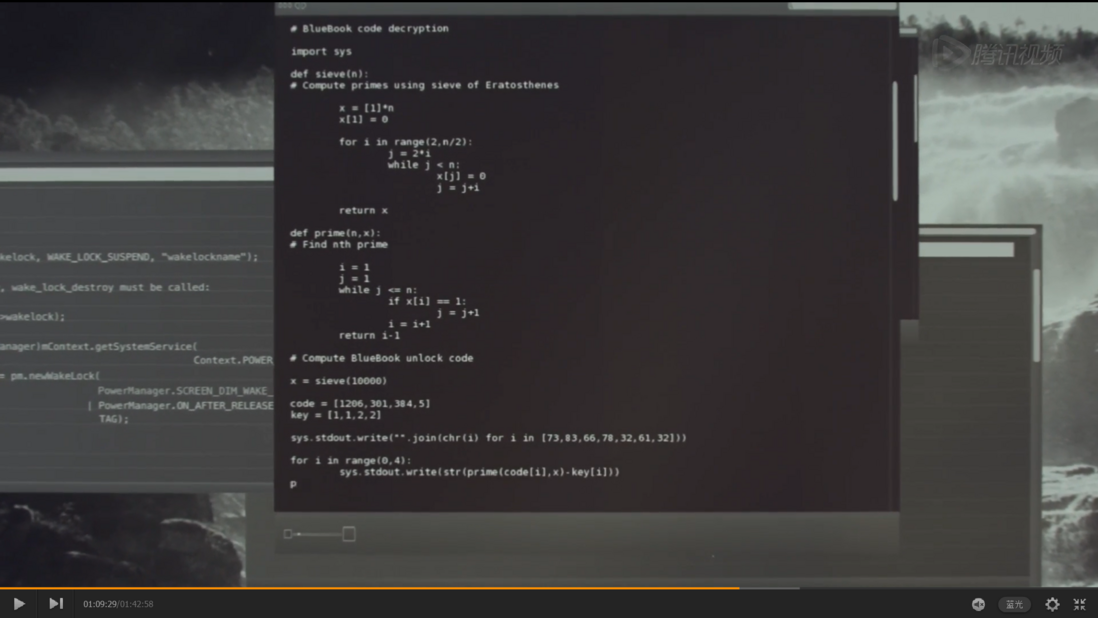
今天看了《机械姬》,探讨人工智能话题的电影,豆瓣评分7.5,还是蛮不错的一部电影。影片1:09:29处出现了一段python代码,细看了一下,发现是筛法求质数的python代码,写得非常简练的。先贴个电影的截图:
影片里的代码略微有点模糊,我重新打一遍,是下面这个样子的
#coding:utf8
import sys
def sieve(n):
#compute primes using sieve eratosthenes
x = [1] * n
x[1] = 0
for i in range(2,n/2):
j = 2 * i
while j < n:
x[j] = 0
j = j + i
return x
def prime(n,x):
#Find nth prime
i = 1
j = 1
while j <= n:
if x[i] == 1:
j = j + 1
i = i + 1
return i-1
x = sieve(10000)
code = [1206,301,384,5]
key = [1,1,2,2]
sys.stdout.write("".join(chr(i) for i in [73,83,66,78,32,61,22]))
for i in range(0,4):
sys.stdout.write(str(prime(code[i],x)-key[i]))代码的最后打印出来下面这个很奇怪的东西,目测是一本书的ISBN,上豆瓣查了一下,是Embodiment and the Inner Life,是关于思维、意识的内容的,和本片的主题息息相关。
ISBN =9780199226559[Finished in 0.1s]
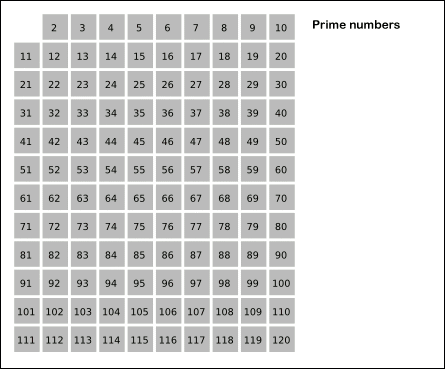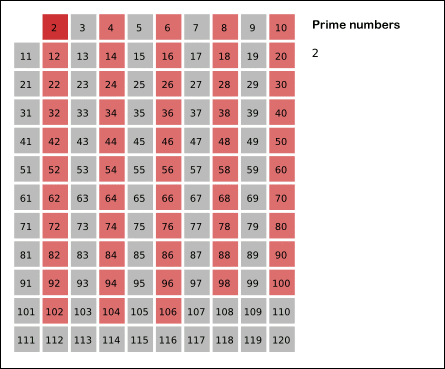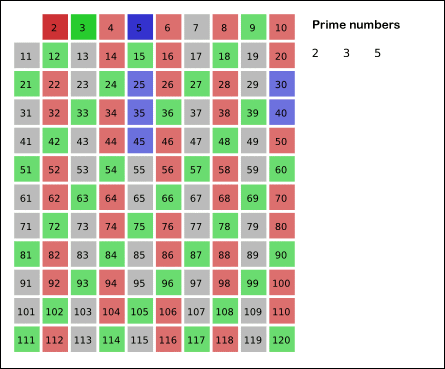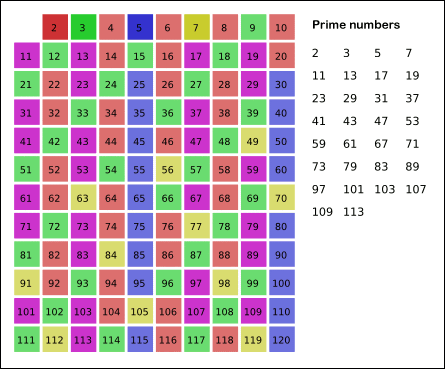
重点还是前面的两个函数实现的筛法求质数。首先介绍一下什么是筛法,筛法相传是古希腊的埃拉托斯特尼发明的一种检测素数的算法。筛法的思路非常简单,可以用下面的动图来描述。给定一个范围,首先用2去筛,把所有2的倍数都筛掉,然后再用3筛,用5筛,不断重复下去......
再来看代码
def sieve(n): //对n以内的数进行筛选,返回一个长度为n的布尔数组 #compute primes using sieve eratosthenes x = [1] * n //定义长度为n的布尔数组(实际上电影里用1和0来表示true和false了) x[1] = 0 //1既不是素数也不是合数,设为0 for i in range(2,n/2)://i从2开始一直到n/2 j = 2 * i //j从2倍i开始 while j < n: x[j] = 0 //把所有i的倍数筛除 j = j + i //下一个i的倍数 return x //返回数组 def prime(n,x): //求第n个素数,只需要在筛选好的布尔数组中找第n个标记为1的数就可以了 #Find nth prime i = 1 //初始化为1 j = 1 while j <= n: //在布尔数组中寻找第n个标记为1的数 if x[i] == 1: j = j + 1 i = i + 1 return i-1 //前面循环中i多加了一次,返回时需要减1
可以看到,使用筛法求第n个质数的时间复杂度为O(n),缺点在需要提前求得筛选的结果,增加了空间复杂度,筛选结果可以用比特位来表示以节省空间。
此外还有一个问题,在求第n个质数的时候,如何要确定第n个质数的大致范围,以确定筛选结果的布尔数组长度。根据素数定理,可以用来估算某个范围内的素数个数,可以用公式x/ln(x)来描述,ln表示自然对数,假设要估计10000以内有多少质数,代入公式10000/ln(10000)得到的结果为1085.73,使用上面的筛法得到的10000以为的质数个数为1229,可以看到估计值比实际值略小一点,估计的范围越大,估计值与实际值的误差越小。实际使用中可以通过公式计算估计值,然后按一定百分比扩大范围即可。
文章转自: http://segmentfault.com/a/1190000004162829